What is Tail Risk?
Tail risk is the risk that an investment will change by more than three standard deviations from its mean.
How Does Tail Risk Work?
Standard deviation is a measure of how much an investment's returns can vary from its average return. It is a measure of volatility and in turn, risk. For math-oriented readers, standard deviation is the square root of the variance.
Let's assume that you invest in Company XYZ stock, which has returned an average 10% per year for the last 10 years. How risky is this stock compared to, say, Company ABC stock? To answer this, let's first take a closer look at the year-by-year returns that compose that average:
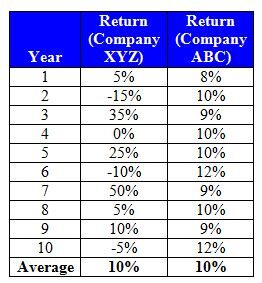
At first look, we can see that the average return for both stocks over the last 10 years was indeed 10%. But let's look in a different way at how close XYZ's returns in any given year were to the average 10%:
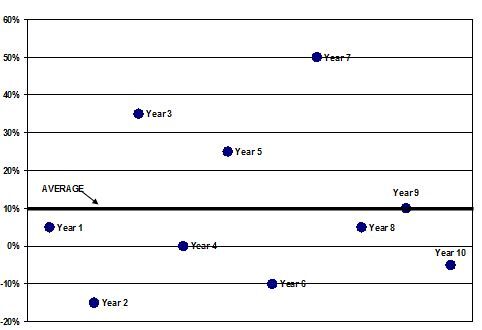
As you can see, only during year 9 did XYZ return the average 10%. In the other years, the return was higher or lower -- sometimes much higher (like in year 7) or much lower (like in year 2). Now look at the annual returns on Company ABC stock, which also had a 10% average return for the last 10 years:
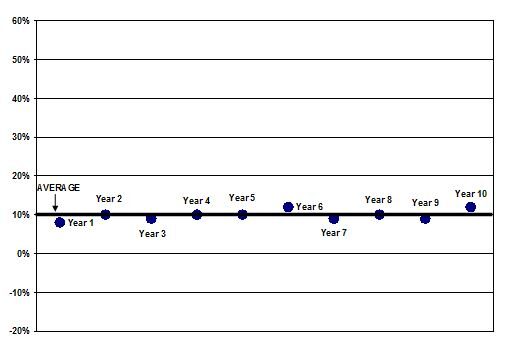
As you can see, Company ABC also averaged 10% return over 10 years but did so with far less variance than Company XYZ. Its returns are more tightly clustered around that 10% average. Thus, we can say that Company XYZ is more volatile than Company ABC's stock is. Standard deviation seeks to measure this volatility by calculating how 'far away' the returns tend to be from the average over time.
For instance, let's calculate the standard deviation for Company XYZ stock. Using the formula above, we first subtract each year's actual return from the average return, then square those differences (that is, multiply each difference by itself):
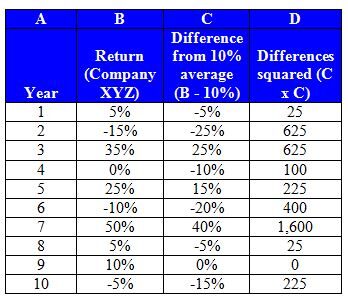
Next, we add up column D (the total is 3,850). We divide that number by the number of time periods minus one (10-1=9; this is called the 'nonbiased' approach and it is important to remember that some calculate standard deviation using all time periods -- 10 in this case rather than 9). Then we take the square root of the result. It looks like this:
Standard deviation = √(3,850/9) = √427.7778 = 0.2068
This means that when Company XYZ stock moves away from its average return of 5%, it usually does so by 20 percentage points. Using the same process, we can calculate that the standard deviation for the less volatile Company ABC stock is a much lower 0.0129 -- it usually deviates from its average by only 1.29 percentage points.
Tail risk is the risk that a stock will deviate by more than three standard deviations from its mean. For Company XYZ, the tail risk is that the stock return changes by more than 60 percentage points; for Company XYZ the tail risk is that the stock return changes by about 4 percentage points.
Why Does Tail Risk Matter?
The probability that a return will change by three standard deviations is very, very low; tail risk is the higher-than-expected risk that it will happen.
In those rare situations in which a stock return moves by that much, as our examples show, the consequences can be very dramatic for a stock with a high standard deviation and not much to worry about for a stock with a low standard deviation. This is bad when returns go down, but it can create overnight wealth if returns go up on a high-standard-deviation stock. For these reasons, some hedge funds have created indexes and other products designed to generate big returns when market volatility increases.



