What Is Bond Duration?
A bond’s duration is a measure of the bond’s sensitivity to interest rate changes. Duration may also be thought of as a measurement of interest rate risk.
It's common for new bond investors to confuse the financial term “duration” with the length of time until a bond is repaid. The repayment date (or the date when the bond’s face value must be redeemed by the borrower) is called the maturity date.
What Are Bonds?
Bonds are considered fixed-income instruments. A bond represents a loan to a borrower from a lender. Borrowers issue or sell bonds when they need to borrow. In return for purchasing the bond, the investor (lender) receives interest at a fixed rate. Regular interest payments (called coupons) are made to the bondholder.
Who Issues Bonds?
Companies, state and city municipalities, and even national governments issue bonds to raise funds for major projects. Investors who purchase bonds become creditors of the issuer.
When bonds are issued, they are issued for a fixed amount, called the principal. The principal is the amount of the loan that must be repaid to the bondholder on the bond’s maturity date. Bondholders receive the coupon (payments of interest on the bond). If the bondholder holds the bond until the maturity date, it can be redeemed for its face value or sold before that date.
How Duration Affects Bond Prices
Bond prices rise and fall inversely with interest rates. In other words, as interest rates rise, bond prices fall (and vice-versa).
The duration of a bond reflects its risk or sensitivity to interest rate changes. Most bonds are issued with a maturity in years, which extends the period of repayment and opens the bond to the risk of changing interest rates.
Current interest rates will likely remain fairly stable from one year to the next, but no one can predict where interest rates will be in three, five, or 10 years.
Remember: The greater the bond duration, the greater the risk that the bond price will drop as interest rates rise.

Why Is Duration Important?
Duration is an important measure of a bond portfolio’s sensitivity to interest rate changes over time. Knowing the duration of a bond helps you compare bond opportunities, assess each bond’s risk, and select the right mix for your portfolio.
Investors who want to capitalize on a trend of falling interest rates may purchase bonds with greater duration. Those who want to buy bonds during periods of interest rate volatility should look for bonds with low duration and high coupons. This minimizes their risk (low duration) and maximizes payments (high coupons).
Calculating Bond Duration
Calculating bond duration by hand (or on a spreadsheet) is time-consuming. Most investors use a bond calculator to quickly assess bond duration. Once each bond’s duration is known, the bonds can be compared, and the investor can create a bond portfolio that addresses their unique risk tolerance and income needs.
Types of Bond Duration
There are three methods to calculate bond duration:
- Macaulay Duration
- Modified Duration
- Effective Duration
Macaulay Duration
Developed by economist Frederick Macaulay in 1938, the Macaulay Duration is the most common method of calculating bond duration. It measures the weighted average time before a bond holder receives the bond’s cash flows. It is often used by bond portfolio managers to calculate risk in an immunization strategy (which will be explained later.)
Calculating the Macaulay Duration
The Macaulay Duration formula reflects the fact that Duration = Present value of a bond’s cash flows, weighted by the length of time to receipt, and divided by the bond’s current market value.
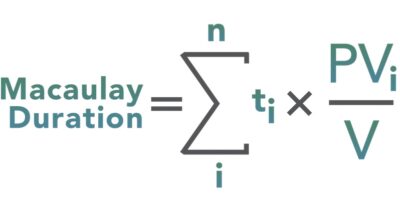
where:
t = period in which the coupon is received
C = periodic (usually semiannual) coupon payment (in $)
y = the periodic yield to maturity or required yield
n = number periods
M = maturity value (in $)
PV = market price of bond (in $)
Macaulay Duration Calculation Example
Let’s assume that Anytown issues a three-year, $1,000 bond with a semiannual 10% coupon. To find the Macaulay Duration, calculate the present value of the cash flows for each period.
Annually, 10% of $1,000 is $100. Our coupon in the example is semiannual, so we divide $100 by 2 = $50.
For the first row, figure in ($50) / (1 + 0.05)^1 = $47.62. For the second row, we'd calculate ($50) / (1 + 0.05)^2 = $45.35. Continue these calculations to fill in the chart:
| Period | Cash Flow | PV of $1 at 5% (semiannual of 10%) | PV of Cash Flows | Period x Cash Flow | Period x PV of Cash Flow |
|---|---|---|---|---|---|
| 1 | $50 | 0.9524 | $47.62 | $50 | $47.62 |
| 2 | $50 | 0.907 | $45.35 | $100 | $90.70 |
| 3 | $50 | 0.8638 | $43.19 | $150 | $129.58 |
| 4 | $50 | 0.8227 | $41.14 | $200 | $164.54 |
| 5 | $50 | 0.7835 | $39.18 | $250 | $195.88 |
| 6 | $1,050 | 0.7462 | $783.53 | $6,300 | $4,701.16 |
| Total | $1,000 | $5,329.48 |
In the table above, cash flows were weighted by the periods in which they occurred, then calculated the present value of each of these weighted cash flows. There are six periods (three years x 2 semiannual payments per year).
To calculate the Macaulay duration, divide the sum of the present values of these cash flows by the current bond price (which we are assuming is $1,000):
Macaulay duration = $5,329.48 / $1,000 = 5.33
Modified Duration
Modified duration is another popular method of calculating bond duration. It measures the price sensitivity of a bond when there is a change in yield to maturity.
How to Calculate Modified Duration
The formula for modified duration uses the Macaulay Duration formula as its base.
Modified Macaulay Duration = Macaulay Duration / (1 + y)
Piggybacking off our earlier calculations in the Macaulay Duration example, we can find the Modified Duration as follows:
Modified Macaulay Duration = 5.33 / (1 + 0.05) = 5.076
Where:
Macaulay Duration = 5.33
Y = 0.05 (semiannual of 10% or 0.10)
As we did with the last example, we apply this result to come up with our change in price (or discount rate in this case):
Approximate Change in Price = 5.076 x 0.002 = 0.010152
That means if the bond had originally sold for $1,000 with a 5% semiannual yield, it would now be selling for $1,000 x (1 - 0.010152) or $989.85. That's a discount from its original $1,000 price.
Effective Duration
The effective duration formula uses the bond's current yield to maturity (YTM), along with two more present values (a slightly higher YTM and a slightly lower yield YTM). This calculation is often used by those who hold callable bonds because the interest rates can change and the bonds may be called before their maturity date.
Effective Duration Formula
Effective Duration = (PL - PH) / (2 x P0 x Change in Yield)
Where:
PL = Price of the bond for the lower yield
PH = Price of the bond for the higher yield
P0 = Price of the bond at its current yield
Using the same example from our earlier table (with interest rates rising 20 basis points, or 10 basis points per semiannual period), we can use discounted present values for each period to ultimately calculate effective duration:
| Period | Cash Flow | PV at 5% | PV at 4.9% | PV at 5.1% |
|---|---|---|---|---|
| 1 | $50 | $47.62 | $47.66 | $48 |
| 2 | $50 | $45.35 | $45.44 | $45 |
| 3 | $50 | $43.19 | $43.32 | $43 |
| 4 | $50 | $41.14 | $41.29 | $41 |
| 5 | $50 | $39.18 | $39.36 | $39 |
| 6 | $1,050 | $783.53 | $788.02 | $779 |
| Total | $1,000 | $1,005 | $994.94 |
Using the sum of cash flows under each calculated PV, plug in the numbers into our effective duration formula:
Effective duration = ($1005.09 - $994.94) / (2 x 1,000 x 0.001) = 5.075
As we did with the last examples, this comes up with our change in price (or discount rate in this case):
5.075 x 0.002 = 0.0105
Again, think of this number as a discount off the original bond price (If yields fell, this number would be a premium on the bond).
So, $1,000 x (1 - 0.0105) = $989.85
Assuming a 0.20% raise in interest rates (or yield), the estimated price of the original bond using effective duration. That’s the same as our modified duration estimate.
Different Types of Duration Strategies
There are four duration strategies for managing bond portfolios.
- Passive
- Index matching
- Immunization
- Dedicated/Active
1. Passive Duration Strategy
A passive duration strategy may be thought of as ‘buy and hold.’ This strategy focuses on long-term objectives and is used by investors who need a stable, reliable income stream. Bonds are chosen based on their coupons and duration is mostly disregarded.
Passive bond portfolios are a traditional and stable method of bond investment while minimizing (or eliminating transaction fees). If started during times of high interest rates, there's a strong chance of outperforming active strategies.
2. Index Matching (Quasi-Passive)
Index matching is a quasi-passive approach to bond investment with the goal of matching the returns and risk of the index. The bond portfolio is built to mimic a bond index (such as the Barclays US Aggregate Bond Index). Although the bonds are bought and often held, an index-matching portfolio needs periodic rebalancing, meaning buying and selling bonds. This strategy incurs more costs through transaction fees – and requires more attention – than passive strategies.
3. Immunization
The immunization strategy blends active and passive strategies. Here, an investor purchases bonds for a specific period of time and disregards changing interest rates.
Investors using the immunization strategy rely heavily on duration estimates to predict the potential volatility of a bond. Insurance companies, pension funds, and other institutional investors may use this strategy, but it is also routinely used by individual investors.
4. Dedicated/Active
Investors using a dedicated/active strategy seek to maximize their overall returns over everything else. They take on more risk, and focus on the future by betting on potential returns instead of settling for a less risky passive strategy. To manage their portfolios, they take multiple interest rates, interest rate anticipation, valuation, timing, and other factors into consideration.
Five Factors that Affect a Bond’s Duration
There are five main factors that impact bond duration:
1. Coupon
The higher a bond's coupon, the more income it produces early on (and the shorter its duration). The lower the coupon, the longer the duration (and volatility). Zero-coupon bonds – which have only one cash flow – have durations equal to their maturities.
2. Maturity
The longer a bond's maturity, the greater its duration and volatility. Duration changes every time a bond makes a coupon payment, shortening as the bond nears maturity.
3. Yield to Maturity
The higher a bond's yield to maturity, the shorter its duration. That’s because the present value of the distant cash flows (which have the heaviest weighting) become overshadowed by the value of the nearer payments.
4. Sinking Fund
The presence of a sinking fund lowers a bond's duration because the extra cash flows in the early years are greater than those of bonds without sinking funds.
5. Call Provision
Bonds with call provisions also have shorter durations because the principal is repaid earlier than a similar non-callable bond.




